Unidad 1. Circuitos RL, RC

 CIRCUITOS RL, RC
Unidad 1.

Un circuito de primer orden se caracteriza por una ecuación diferencial de primer orden. Parecerá muy sencillo, pero los circuitos RC y RL tienen innumerables aplicaciones en el campo de la electrónica, comunicaciones y sistemas de control.

La ecuación diferencial de entrada/salida de un circuito RC o RL es una ecuación de primer orden, como es el caso de la ecuación (1) o de la ecuación (2), presentadas a continuación con su respectivo circuito de origen. Por ello, a los circuitos RC y RL se les denomina de manera genérica, circuitos de primer orden:

Por tanto, Un circuito de primer orden se caracteriza por una ecuación diferencial de primer orden.

Tenemos dos maneras de excitar los circuitos RC y RL. La primera es mediante las condiciones iniciales del capacitor o del inductor, sin necesidad de conectar una fuente de alimentación. La segunda manera es excitar al circuito mediante una fuente independiente. Aplicar el primer método nos permite analizar la respuesta natural del sistema, mientras que gracias al segundo método podemos determinar la respuesta forzada del sistema a una entrada específica, que por lo general es la función escalón unitario. Por ello, consideraremos ambos métodos para cada tipo de red (RC o RL).

Circuito RC sin fuente

Considere el circuito RC de la Figura 3. Obtenemos este circuito cuando la fuente independiente, conectada como en la Figura 1, se desconecta súbitamente:

Los pasos necesarios para analizar la respuesta de un circuito RC sin fuente son:

1. Determinar el valor de la tensión vc(t) en el capacitor en el tiempo t=0 seg;
2. Hallar el valor de la constante de tiempo τ.

El parámetro más relevante de un circuito de primer orden es la constante de tiempo τ. En el caso de un circuito RC:

La constante de tiempo τ de un circuito RC descargándose es el tiempo requerido para que la respuesta del sistema a la entrada escalón, disminuya en un factor de 1/e, es decir, 36.8% de su valor inicial. La etapa en la cual el capacitor descarga toda su energía en el circuito RC es conocida como Fase de Descarga. Veamos cómo funciona.

En el circuito de la Figura 3, cuando se desconecta la fuente en el instante inicial to= 0 seg, la energía acumulada en el capacitor está al máximo según su capacidad y por ende la tensión vc(t) en el en el capacitor en el tiempo inicial to= 0 seg es vc(t) =vc(o). Es también a su valor máximo Vo. Es decir:

Aplicando La Ley de Corriente de Kirchhoff (LCK) en el circuito de la Figura 3, obtenemos:

Sabemos por definición que:

Sustituimos estas últimas fórmulas en la ecuación (5):

Se puede demostrar que la solución a la ecuación diferencial (6) es la siguiente:

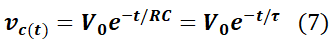
 podemos ver la respuesta natural de un circuito RC en Fase de Descarga, donde el voltaje en el capacitor cae exponencialmente, y en el tiempo t=τ, el voltaje ha caído 36.8% de su valor máximo. Es decir:

VIDEOS RELACIONADOS